Teorema de Euclides

El origen, demostración ,enunciados, aplicaciones y problemas resueltos acerca del «Teorema de Euclides».

El teorema de Euclides es muy antiguo y fue descubierto por un matemático griego con el mismo nombre hace ya más de dos mil años pues este de hombre vivió entre los años 325 a.c.-265 a.c., el teorema ha tenido extensa aplicación pues de cierta forma completa la comprensión de las relaciones geométricas existentes en el triángulo rectángulo relacionando los catetos del triángulo con sus proyecciones en la hipotenusa.

Origen y demostración

Euclides se dió cuenta de que al trazar la altura con respecto a la hipotenusa en un triángulo rectángulo se da origen a dos triángulos más aparte del original , los cuales entre si son semejantes y a la vez son semejantes también con el triángulo original , lo que implica que sus lados homólogos respectivos son proporcionales.

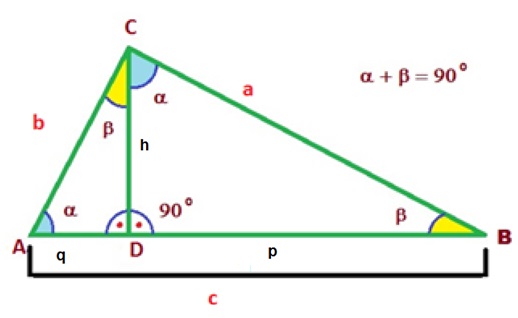
A continuación se muestra gráficamente la altura trazada desde la hipotenusa en el triángulo rectángulo y los triángulos que nacen a partir de su trazado :

Se puede apreciar los ángulos que son congruentes en los triángulos de esta forma se puede verificar la semejanza existente entre los tres triángulos involucrados según el criterio de semejanza AAA , que dice que si dos triángulos tienen todos sus ángulos iguales son semejantes.

Luego de demostrar que los triángulos son semejantes es posible establecer las siguientes proporciones:

Teorema de Euclides referido a un cateto

En cualquier triángulo rectángulo la medida de cada uno de los catetos es media proporcional geométrica entre la hipotenusa y la proyección del cateto sobre ella.

$\frac{c}{a}=\frac{a}{p}\rightarrow a^{2}=c\ast p$ $\frac{c}{b}=\frac{b}{q}\rightarrow b^{2}=c\ast q$

Teorema de Euclides referido a la altura

En cualquier triángulo rectángulo la altura trazada según la hipotenusa es media proporcional geométrica entre los segmentos que determina esta sobre la hipotenusa.

$\frac{q}{h}=\frac{h}{p}\rightarrow h^{2}=q\ast p$

Además, mediante un procedimiento algebraico entre las ecuaciones del teorema se puede demostrar que :

$h=\frac{a*b}{c}$

Aplicaciones

Desde que se propuso hasta la fecha el teorema de Euclides ha sido enseñado sin cesar en las escuelas y universidades modernas de todo el mundo, pues posee una extensa gama de aplicaciones en diversas ramas del saber que usan matemáticas como ciencias ingenieriles, física, química y astronomía por lo cual la dimensión de su aporte es incalculable.

Ejercicios resueltos del Teorema de Euclides

1.- Considere que en el triángulo que se muestra en la figura 1 la altura con respecto a la hipotenusa tiene un valor de 10 cm , y el segmento q tiene un valor de 5 cm , obtenga el valor del segmento p.

Para la resolución de este problema se usará el teorema de Euclides referido a la altura que nos dice que:

$h^{2}=p*q$

por lo tanto reemplazando con los valores otorgados por el problema se tiene que:

$(10cm)^{2}=p*5 cm$

desarrollando la potencia y despejando «p» se tiene que

$p=\frac{100}{5}=20 cm$

2.- Considere que en el triángulo de la Figura 1 el cateto a mide 4 cm y la hipotenusa c mide 5cm, calcule la proyección del cateto sobre la hipotenusa.

Para resolver este problema se usará el «Teorema de Euclides referido a los catetos» el cual nos dice que:

$a^{2}=c*p$

reemplazando con los valores otorgados por el problema se tiene que :

$(4cm)^{2}=5cm*p$

desarrollando la potencia y luego despejando «p» se tiene que :

$p=\frac{16}{5}=3.2cm$

3.- Considere que en el triángulo de la figura 1 el valor de «q» es 1,8 cm y el valor de la hipotenusa «c» es de 5 cm , calcule el valor del cateto «b».

Para resolver este problema se usará el «Teorema de Euclides referido a los catetos» el cual nos dice que :

$b^{2}=c*q$

reemplazando con los valores otorgados por el problema se tiene que:

$b^{2}=1.8*5$ $b^{2}=9$

b=3