El Círculo

Anteriormente vimos la circunferencia, conocimos sus elementos y descubrimos una importante propiedad que involucra a los ángulos que podemos dibujar dentro de ella. Ahora avanzaremos y estudiaremos el círculo.

¿Qué es un círculo?

A modo de definición, el círculo corresponde a la superficie que se encuentra encerrada por la circunferencia. Dicho de otro modo, la circunferencia correspondería a la frontera del círculo.

Basados en esto, podemos distinguir las siguientes regiones:

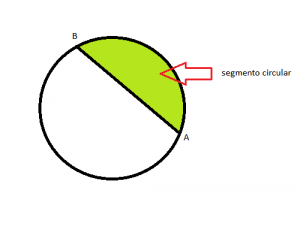
Segmento circular: es la porción de círculo que está delimitado por una cuerda y el arco que está entre los dos puntos extremos de ésta.

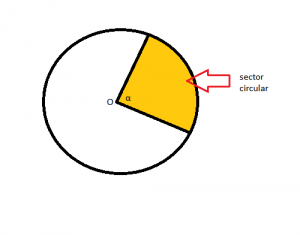
Sector circular: es la porción de círculo delimitada por dos radios y el arco comprendido entre ellos.

En la vida diaria encontramos muchos ejemplos de esto, uno de ellos es el siguiente: si nos fijamos en la forma que tiene una pizza, descubriremos que tiene justamente forma de círculo; cada trozo en que la dividimos corresponde a un sector circular.

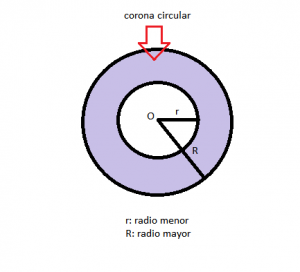
Corona circular: corresponde a la región que está delimitada por dos círculos concéntricos (es decir, tienen el mismo centro, pero sus radios son diferentes).

Determinando

Ya que conocemos el diámetro de una circunferencia, podemos hacer un sencillo experimento: con un trozo de cuerda y una regla, podemos medir el diámetro y el contorno de diferentes objetos con forma circular. Una vez anotadas todas las medidas en una tabla, para cada objeto se procede a dividir la medida de su contorno por la medida de su diámetro. Lo sorprendente es que el resultado de cada división tiende a un número en particular: 3,14.

Este número se llama (se lee «pi») y es un decimal con parte decimal infinita y no periódica (ningún dígito se repite en forma consecutiva), y si redondeamos al quinto dígito decimal queda . De acá en adelante  nos va a servir para calcular el perímetro de la circunferencia y el área del círculo, además de sus diferentes regiones.

Perímetros y áreas

a) El perímetro de la circunferencia (P) es igual a: , siendo  la medida del radio.

b) Si queremos calcular el área del circulo (A), tenemos que multiplicar  por el radio al cuadrado

c) Área del sector circular:

donde  es la medida del ángulo en grados sexagesimales.

Lo que sigue es ir un poco más allá y preguntarnos ¿cuánto espacio ocupa una pelota? ¿y un tarro de conserva? En ese sentido  nos seguirá siendo muy útil.