Función cuadrática

Conoce la definición y elementos de la función cuadrática, cuáles son sus los elementos y cuál es su representación gráfica en el plano cartesiano.

Una función cuadrática es una función que se representa en el plano cartesiano por una parábola, la forma y posición se puede determinar a partir de los elementos de la función cuadrática.

Definición de la función cuadrática

Diremos que una función cuadrática tiene la siguiente forma:

$\ ax^2+bx+c$ con «a»,»b»,»c» enteros y «a» distinto de 0.

Si el coeficiente “a” fuera cero, la ecuación pasaría de una función cuadrática a una lineal, por eso es importante el detalle de la definición.

Elementos de la función cuadrática

Concavidad:

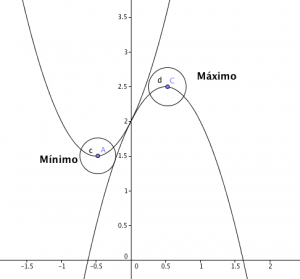
La concavidad nos indica si la parábola abre hacia arriba o hacia abajo sus ramas, si el coeficiente “a” es mayor que cero, la parábola abre hacia arriba, si el coeficiente “a” es menor que cero, la parábola abre hacia abajo.

Veamos la representación gráfica de las siguientes funciones:

$\ 2x^2+2x+2$ y $\ -2x^2+2x+2$

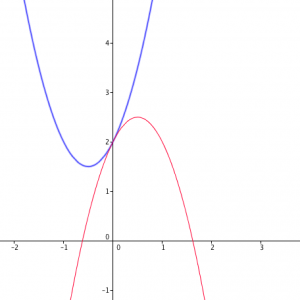
Concavidad

En azul la parábola que abre hacia arriba y en rojo la parábola que abre hacia abajo.

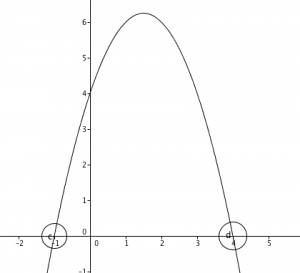
Raíces

Las raíces de una función cuadrática son los valores de x cuando la función es igual a cero. En otras palabras son los valores de x donde la parábola intersecta el eje x, también puedes encontrar las raíces con el nombre de soluciones o ceros. Generalmente para encontrar las raíces, podemos factorizar la función o bien utilizar la fórmula de Baskara, que tiene la siguiente forma.

$\ x=\frac{-b \pm \sqrt[2]{b^2-4ac}}{2a}$

Ejemplo:

Buscaremos las raíces de la función $\-x^2+3x+4$

Las soluciones de la ecuación cuadrática serán x = -1 y x = 4.

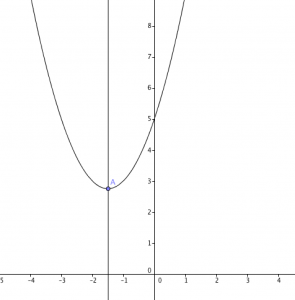
Vértice

El vértice es un punto de la parábola máximo o mínimo en la función. Diremos que el vértice es máximo si la parábola tiene concavidad hacia abajo y diremos que el vértice es mínimo siempre y cuando la parábola tenga concavidad hacia arriba.

La fórmula para encontrar el vértice es la siguiente:

V=( $\frac{-b}{2a},\frac{4ac-b^2}{4a}$ )

Eje de simetría

El eje de simetría es una recta paralela al eje y que pasa por el vértice de la parábola, por tanto es única y dividirá en dos partes iguales a la parábola como una simetría axial. El eje de simetría se representa por la recta x = -b/2a.

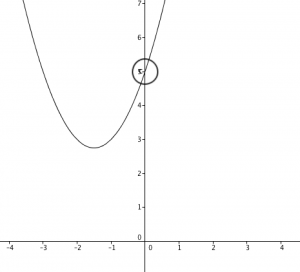
Corte con el eje y

El corte con el eje y está determinado por el coeficiente “c”, el punto de intersección será el punto (0, c).

Para poder hacer una correcta gráfica de una parábola se deberá contemplar todos los elementos antes mencionados, así se logrará realizar un completo bosquejo de la función cuadrática.