Geometría de Proporción II: Semejanza y más
Semejanza de Triángulos
Por definición, dos triángulos se dicen semejantes (no congruentes) si tienen la misma forma pero no la misma área
Para poder determinar si dos triángulos son semejantes tenemos los siguientes criterios:
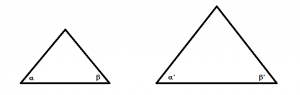
1.- Dos ángulos iguales
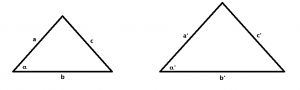
2.- Un ángulo igual entre dos lados proporcionales
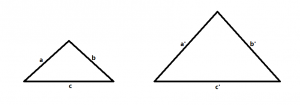
3.- Tres lados proporcionales
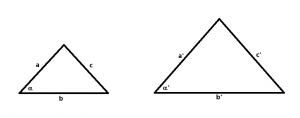
4.- Dos lados proporcionales y el ángulo opuesto al mayor de ellos igual
División de Segmentos
Si tenemos un segmento de longitud , podemos ocupar las proporciones para determinar en qué razón dividirlos y así lograr que cada segmento tenga una cierta longitud.
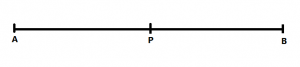
a) División interior
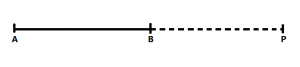
b) División exterior