Homotecia
Descubre qué es homotecia y las propiedades de la homotecia.
Definición de Homotecia
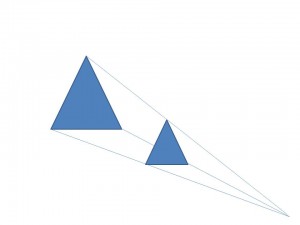
La homotecia consiste en la transformación de figuras geométricas en un plano o espacio vectorial. Esto sucede tomando como referencia un punto y proyectando desde éste rectas que pasen por los vértices de las figuras.
Al unir las resultantes rectas proyectadas desde los vértices en un solo punto, este punto se conoce como centro de homotecia.
En la homotecia existe una figura y su «sombra» o figura homotética, la cual dependiendo de la distancia que queden una de otra sus relaciones de tamaños pueden ser distintas, esta relación de tamaños depende del factor de homotecia (o razón de homotecia).
Dentro de las representaciones gráficas el Centro de Homotecia es identificado con la letra «C», mientras que en el caso del factor de homotecia es usualmente simbolizado con la letra «k».
Propiedades de la Homotecia
Las principales propiedades de la homotecia son cinco, en resumen:
1. Homólogo. Una figura es homóloga a otra siempre y cuando la figura homotética no varíe su tamaño independiente de la distancia en que se configure una y otra.
2. Factor 0<k<1. Si el Factor Homotécico está entre cero y uno, entonces la figura homotécia se sitúa entre el centro y la figura original. En este caso la figura homotécica es de inferior aspecto a la figura original.
3. Factor k>1. Si el factor Homotécico es mayor que uno, entonces la figura homotécica se sitúa a mayor distancia del centro homotécico que la figura original. En este caso, la figura homotécica se suele ver en los diagramas con un aspecto superior o más grande que la figura original.
4. Factor k<0. Si el factor Homotécico es menor que cero, o sea, si es negativo, entonces la figura homotécica será una proyección de una imagen de la figura original (esto es, la visualización de la figura como si se invirtiera en relación a la figura original).
5. Paralelismo. Dentro del plano en que se configuran las figuras, siempre se da que de existir figuras en dos dimensiones con lados (ejemplo: triángulos, trapecios, rectángulos, cuadrado, etc); entre ambas figuras (la figura original y la figura de homotecia) se dan paralelismos entre los lados entre una figura y otra.
Importante: La homotecia también puede operar con circunferencias, en este caso los trazos de referencia no son los lados, sino el radio y/o el diámetro.