Nociones de funciones

Conoce que son las funciones, sus fundamentos básicos a partir del modelamiento y la representación gráfica de estas.

¿Que es una función?

Una función es una relación entre dos variables que interactúan mutuamente representando una situación particular.
Constantemente en la vida cotidiana tenemos situaciones a las cuales podríamos darles un modelamiento matemático, por lo general en estas situaciones, sin darnos cuenta, generamos soluciones relacionando y planteando funcionamientos numéricos casi implícitos.
Por ejemplo:

En una bencinera de un pueblo venden la gasolina de 95 octanos a 800 pesos el litro, en una tabla se hace el siguiente registro entre los litros de bencina y el total a pagar.

Litros	Pesos
1	800
2	1600
3	2400
4	3200
5	4000
6	4800

En una  función tendremos generalmente dos variables, una será la variable independiente y la otra será la variable dependiente, que valga la redundancia, dependerá de la otra. Asociaremos a la variable independiente la notación en el eje x, en tanto a la variable dependiente le asignaremos la notación en el eje y.

Entonces?, ¿cuáles son las variables y cuál será dependiente o independiente?

Las variables que trabajamos son la bencina y los pesos. Entonces para saber cual es dependiente debemos preguntarnos ¿cuál es la que depende de la otra? para saber el valor total a pagar, debemos saber cuantos litros de bencina compraremos. Por lo tanto, el valor de la bencina depende de la cantidad de litros que se compren, por lo que la variable independiente serán los litros y la variable dependiente serán los pesos.

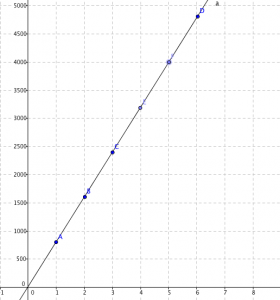
Si pasamos los datos a un gráfico obtendremos lo siguiente.

Entonces ahora podemos modelar la situación y escribir la función asociada a esta:

 Valor bencina(pesos)=800 * cantidad de bencina(litros)

Finalmente logramos generar una función que nos ayudará a saber el valor de la bencina para una cantidad de litros determinada. Recuerda que podemos plasmar esta situación en un gráfico donde el eje x se ocupará para la variable independiente y el eje y para la variable dependiente. Además,si no recuerdas como trabajar con el plano cartesiano, puedes complementar tu conocimiento revisando el contenido «plano cartesiano, punto y vector».

Recuerda que tu mismo puedes modelar situaciones que te van pasando en el día y así descubrir lo cerca que están las funciones de tu quehacer cotidiano.