Números Decimales

Los números decimales forman parte del conjunto de números racionales y los utilizamos en variadas ocasiones de nuestra vida diaria. Algunas veces estos se asocian a índices económicos, como cuando decimos que el dólar se encuentra a 521,1 centavos o que el IPC subió en un 1,1%, pero también los utilizamos al referimos a números que no son exactos, como cuando hablamos de que en el supermercado compramos 2,5 kilos de carne o decimos que estamos pesando 59 kilos y medio.

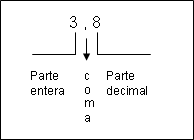
Como podemos ver en el siguiente cuadro, los números decimales se encuentran formados por una parte entera, una coma y una parte decimal.

Cuando leemos números decimales, a la parte entera le llamamos unidad, luego mencionamos la coma (que separa a la parte entera de la parte decimal) y finalmente decimos el número que sigue a la coma. En el caso anterior, diríamos que el número al cual nos referimos es el tres coma ocho, sin embargo, también podemos hablar de tres coma ocho décimos, ya que dependiendo de la posición en que se encuentre el número que sigue a la coma, el lugar en que éste se encuentre.

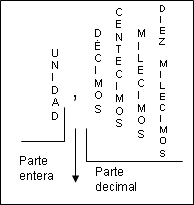
Según el cuadro anterior, podemos ver que si el número se encuentra una posición al lado de la coma, lo llamaremos décimo; si se encuentra a dos posiciones hablaremos de centésimo; si se encuentra a tres posiciones, hablaremos de milésimo, y así sucesivamente. Esto, ya que si la unidad es dividida en 10, 100 ó 1000, respectivamente, la posición en que quedará el número corresponderá al lugar mencionado anteriormente, tal como muestra el cuadro anterior.

Veamos algunos ejemplos:

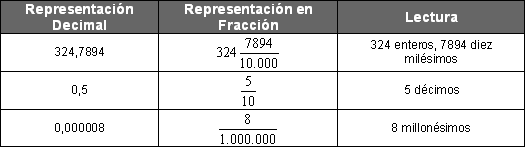
1. La lectura del número 324,7894 será 324 enteros, 7894 diez milésimos
2. La lectura de 0,5 será 5 décimos
3. La lectura de 0,000008 será 8 millonésimos

Para clarificar más aún la lectura de los números decimales, haremos un nexo con la representación de éstos en fracciones, en donde lo que hacemos es dividir la unidad por múltiplos de 10.

Decimales en la recta numérica

Si observas una regla, puedes notar que la unidad se encuentra dividida en 10 partes iguales, tal como lo vemos en la siguiente recta:

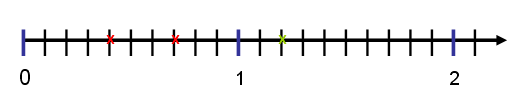
Si consideramos (desde ahora escribiremos las fracciones así: 4/10), nos ubicaremos en la división: 0,4

Si consideramos 8/10 (ocho décimos), nos ubicaremos en la 8º división: 0,8

Ahora bien, cuando una fracción considera una parte entera nosotros debemos situarnos desde ahí y después ubicar los décimos. Por ejemplo, si tenemos 1 entero y 2/10 (dos décimos), sabemos que hay 1 entero, situándonos por lo mismo entre el 1 y el 2, para luego ubicar la parte decimal en la recta numérica.

Y así sucesivamente…

Fracciones de denominador 100 y porcentaje

Otra manera de representar la relación existente entre dos cantidades son los porcentajes, los cuales pueden tener una representación decimal o fraccionaria.

Los porcentajes son fracciones con denominador 100, por lo mismo trabajar con ellos se hace muy fácil. Así por ejemplo, vemos que si queremos pasar un número expresado como porcentaje a fracción, tenemos que escribir una fracción con denominador 100 y el numerador que corresponda según el número expresado. Así por ejemplo, la fracción correspondiente a 14% es 14/100.

Siguiendo con el ejemplo anterior, realizaremos el paso de fracción a número decimal. Por lo tanto, es lo mismo que decir 14 de 100 o 14:100 = 0,14. Lo que hacemos en este caso, es correr la coma tantas veces como ceros tenga el denominador. Vemos que el 100 tiene 2 ceros, por lo que desplazaremos la coma dos espacios a la izquierda y obtendremos 0,14. Ahora bien, en el caso de que la fracción considerada no tenga como denominador a un múltiplo de 10, basta con dividir el numerador entre el denominador. Por ejemplo, en la fracción 3/6 (tres sextos), tenemos que el resultado de su división es 0,5 (ó 3:6).

El uso que se le da a los porcentajes generalmente responde a los resultados obtenidos de una muestra, y se aplica a investigaciones o encuestas. Por ejemplo, si tenemos que en las últimas elecciones del centro de alumnos de tu colegio, que el 56% votó por la lista 2, eso significa que de cada 100 alumnos, 56 votaron por dicha lista, lo cual también podemos expresarlo como fracción en 56/100.

Equivalencia de decimales y fracciones

Es indudable la relación existente entre los números decimales y las fracciones, esto, ya que es posible expresar una misma cantidad como número decimal o fracción. Ahora bien, al hecho de que podamos expresar una misma cantidad de dos maneras diferentes le llamamos equivalencia, debido a que las dos maneras que tenemos de expresar dicha fracción corresponden a la misma cantidad de elementos.

Algunos ejemplos de decimales equivalentes a fracciones pueden ser representados tanto en la recta numérica como en figuras achuradas. Así, si tenemos el decimal 0,5 vemos que su representación fraccionaria es 5/10, o bien 1/2 al ser simplificado. Por lo que ubicamos al decimal 0,5 en el medio, entre el 0 y el 1, tal como muestra la recta.

Decimales periódicos y semiperiódicos

Anteriormente mencionamos que para encontrar la expresión decimal de una fracción basta con dividir el numerador por el denominador de ésta, y dimos como ejemplo a la fracción 3/6, cuya división da como resultado 0,5 (ó 3:6). Ahora bien, vemos que no siempre el resultado que nos da la división de una fracción resulta ser un número exacto, cuando esto ocurre, hablamos de decimales periódicos o semiperiódicos.

• Los decimales periódicos, son aquellos en donde se repiten sucesivamente los mismos números de un decimal. Así por ejemplo, vemos que el cociente de la fracción 2/11 (dos onceavos), es 0,18181818… , donde al grupo de cifras que se repiten se les llama período (en este caso 18) y la manera en que se escribe es 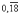y la barra abarca el bloque de cifras que se repite sucesivamente
• Por otro lado, vemos que también existen los decimales semiperiódicos, los cuales tienen una parte decimal no periódica y otra que si lo es. Así por ejemplo, vemos que el decimal 1,34555555… sólo tiene al 5 repetido indefinidamente (el cual vendría a ser su parte periódica), mientras que el 34 no forma parte de ese período. La manera en que escribimos dicho decimal es 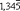, donde la barra sólo abarca al bloque de cifras que se repite indefinidamente.

Adición y sustracción de números decimales

La adición y sustracción de decimales es muy similar a la que hacemos con los números naturales, sin embargo, ahora debemos ser más ordenados y colocar en columna la parte entera y la decimal, de modo que siempre se encuentre una coma bajo la otra.

Ejemplo: 3,7 + 5,84

3,7
+ 5,84
9,54 o bien, 9 enteros 54 centésimos.

Ejemplo: 5,15 – 1,12

5,15
– 1,12
4,03 o bien, 4 enteros 3 centésimos.