Números Racionales
Características de los números racionales: la suma, resta, multiplicación y división de éstos; fracción impropia y fracción mixta.
Números Racionales. (Conjunto Q)
Los números racionales son números no enteros. Los componen las fracciones de resultado no entero.
Características de una Fracción
- Una fracción en sí, es una división.
- Una fracción está compuesta por un numerador (el número de arriba) y el denominador (el número que va abajo).
- La línea intermedia que separa el numerador del denominador se conoce como línea divisoria.
- Usualmente tanto el numerador como el denominador son números enteros, no decimales.
- Puede ser positiva o negativa.
Suma y Resta de Racionales o Fracciones.
Para sumar dos fracciones:
- Se multiplican los denominadores de ambas y el resultado queda anotado abajo de la línea divisoria.
- Se multiplica el numerador del primer término por el denominador del segundo término (cruzado) y se anota el resultado sobre la línea divisoria.
- Se multiplica el denominador del primer término por el numerador del segundo término (cruzado) y se anota el resultado sobre la línea divisoria.
- Los resultados de 2 y 3 apuntados sobre la línea divisoria, son sumados.
Para restar dos fracciones:
- Se multiplican los denominadores de ambas y el resultado queda anotado abajo de la línea divisoria.
- Se multiplica el numerador del primer término por el denominador del segundo término (cruzado) y se anota el resultado sobre la línea divisoria.
- Se multiplica el denominador del primer término por el numerador del segundo término (cruzado) y se anota el resultado sobre la línea divisoria.
- Los resultados de 2 y 3 apuntados sobre la línea divisoria, son restados.
Multiplicación y División de Racionales o Fracciones.
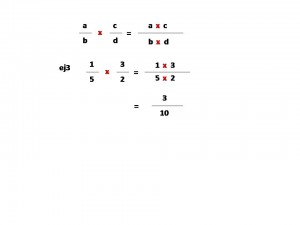
Para multiplicar dos fracciones:
- Primero multiplicar el numerador del primer término, por el numerador del segundo término.
- El resultado se anota como un numerador.
- Luego multiplicar el denominador del primer término, por el denominador del segundo término.
- El resultado se anota como el denominador.
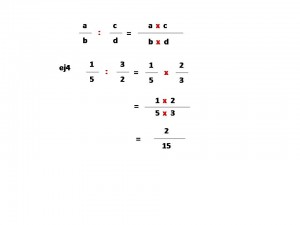
Para dividir dos fracciones:
- El segundo término se invierte, esto es, donde está el numerador se posiciona el denominador y viceversa.
- Luego se resuelve como el caso de una multiplicación de dos fracciones.
Simplificación de Fracciones.
El objetivo de la simplificación de una fracción, es la de reducir tanto el numerador como el denominador al mínimo valor posible.
Para simplificar una fracción:
- Para simplificar una fracción, es necesario primero buscar un número que sea múltiplo tanto del numerador como del denominador.
- Luego se divide por ese número tanto el numerador como el denominador.
Para simplificar dos fracciones:
- Primero se debe fijar que todas las fracciones simplificar estén multiplicándose entre si.
- Luego se puede simplificar «cruzado», se debe encontrar un número que sea múltiplo de un numerador y a la vez de un denominador.
- Este paso se puede seguir repitiendo.
- De otra forma, también se puede simplificar el resultado de la multiplicación de la fracción (ver para simplificar una fracción).
Número Mixto a Fracción Impropia y Fracción Impropia a Número Mixto.
Un número mixto es un número que se compone de una parte entera y una parte fraccionaria. Ejemplos: un entero dos quintos, cinco enteros tres medios, etc.
Una fracción impropia, es la cual al dividir el numerador con el denominador da como resultado un número mixto.
Para obtener un número mixto desde una fracción impropia:
- Se multiplica el número entero con el denominador de la fracción.
- Luego se le suma el numerador.
- Ese resultado es el numerador de la respuesta.
- Se conserva el denominador.
Para obtener una fracción impropia desde un número mixto:
- Se divide el numerador con el denominador.
- El resultado entero es la componente entera.
- El resto quedaría como el numerador.
- El denominador se conserva.