Proporciones Directa e Inversa

Aprende como identificar una proporción y clasificarla según si es una proporción directa o inversa.

¿ Es o no es proporción?

Lo primero que debemos establecer en una relación numérica es que exista siempre una proporción entre los términos que vamos comparar, para eso debemos dividir todas las duplas de términos asociados entre ellos para encontrar así una única razón, si alguna de las duplas al dividir no nos da la razón, diremos que la relación no es proporcional o que no está en proporción.
Si tienes dudas, te recomendamos visitar: razones y proporciones.

Ejemplo:
Estará en proporción la relación?

En un curso de geometría de educación básica analizan las figuras geométricas, en especial la figura del rectángulo. Toman distintos rectángulos de papel y hacen mediciones entre el largo y ancho de cada uno de estos, los resultados arrojados por los estudiantes son los siguientes.

Largo	Ancho
10	5
6	3
8	5

Tomamos las duplas 10–5 / 6–3 / 8–5. Dividiremos el primer termino con el segundo.

• Primera dupla, 10:5= 2, por lo tanto la razón es 2.
• Segunda dupla, 6:3= 2, por lo tanto la razón es 2.
• Tercera dupla, 8:5= 1, 6, por lo tanto la razón es 1,6.

En conclusión, los rectángulos anteriores no son todos proporcionales ya que no comparten la misma razón.

Proporción Directa

Es una relación que debe estar en proporción,  es decir: si una variable crece la otra también debe hacerlo o viceversa.

Analicemos esto con un ejemplo.
Un ciclista viaja en su bicicleta a una velocidad de 12km/h. Recogeremos en una tabla su registro cada una hora.

Distancia en Km	Horas
12	1
24	2
36	3
48	4

Si dividimos los términos de las duplas obtendremos una constante, a la que llamaremos constante de proporcionalidad directa que en este caso es 12.

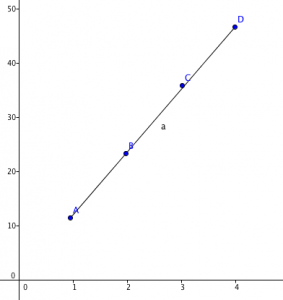
Por lo tanto,  confeccionaremos el siguiente gráfico que es característico de una proporción directa.

Podemos distinguir una proporcionalidad directa en un gráfico tomando en consideración dos cosas importantes, primero el desplazamiento de la gráfica debe ser lineal, es decir se mueve en linea recta y segundo debe tener una pendiente positiva.

Proporcionalidad Inversa

Es una relación que debe estar en proporción, luego si una variable decrece la otra no debe hacerlo o si bien, una variable crece la otra no debe hacerlo.
Veamos un ejemplo para comprender este tipo de proporcionalidad.

En la construcción de un edificio si se trabaja con 200 obreros, la obra tiene fecha para 12 meses, si se trabaja con 150 serán 16 meses de obra, si se trabaja con 100 obreros serán 24 meses de obra, si se trabaja con 50 obreros se demorará 48 meses de obra.

Al traspasar los datos en una tabla tenemos:

Obreros	Meses de obra
200	12
150	16
100	24
50	48

 

Si multiplicamos ambos términos de la dupla, obtendremos la constante de proporcionalidad inversa, que en este caso será 2400.

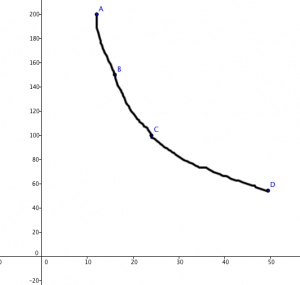
 Podemos distinguir una gráfica característica de este tipo de proporción, puesto la curva va tomando la forma de una hipérbola.

Cuando hablamos de proporción a secas generalmente se refiere a la proporción directa, sin embargo es importante que identifiques también los casos en que existe proporcionalidad inversa a partir de las gráficas y las características específicas antes mencionadas.