Transformaciones Isométricas
Conoce qué es la Isometría, el concepto de translación, rotación, simetría o reflexión. Además, simetría axial y simetría Central.
Isometría
La palabra isometría proviene del griego iso, que significa igual o mismo. dicho de otra forma, también se puede decir que dos figuras geométricas son isométricas si tienen la misma medida.
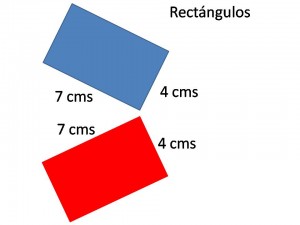
En el esquema que se muestra a continuación podríamos decir que el rectángulo rojo y el rectángulo azul son isométricos entre sí (o sea, que ambos tienen las mismas medidas).
Transformación Isométrica.
Una transformación isométrica es cuando una de las figuras que se están analizando se modifican sin variar sus medidas, en la transformación isométrica solamente varía la posición de una figura en relación a la otra.
Existen tres tipos de variaciones isométricas.
- Traslación.
- Rotación.
- Simetría o Reflexión.
Transformación Isométrica por Traslación.
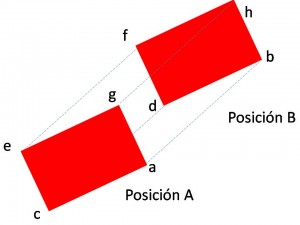
Para que una transformación isométrica por translación se cumpla, se tiene que dar la condición de que la figura que se trasladó no cambie su orientación en relación a la posición inicial y tampoco debe perder sus medidas internas, ni de ángulos ni de lados. Es decir, si lo representamos mediante un esquema, los trazos ab, cd, ef y gh deben ser paralelos:
Transformación Isométrica por Rotación.
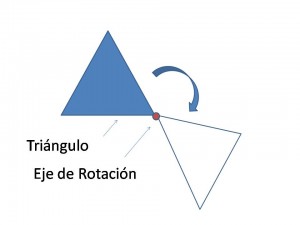
Para que se cumpla una transformación isométrica por rotación, es necesario que la figura geométrica gire en torno a un eje previamente definido manteniendo sus medidas internas, tanto de ángulos como de lados. Observar el siguiente esquema:
Transformación Isométrica por Simetría o Reflexión.
Para describir la transformación isométrica por simetría o reflexión, ejemplificaremos utilizando algo que es conocido por todos: una imagen y su reflejo en un espejo. Para que exista simetría o reflexión es necesario que dos figuras geométricas sean idénticas como si una se reflejara una de ellas en un espejo.
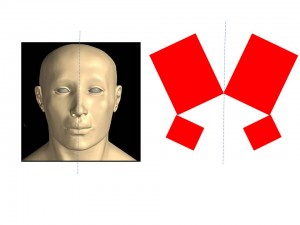
La simetría se da de forma natural en muchos aspectos de la naturaleza, si observamos un rostro y dibujamos una línea recta entre el medio de la frente hasta en medio del mentón, nos daremos cuenta que las dos mitades que quedan es como si existiera un espejo en medio. Ahora bien, si hacemos el experimento de instalar el espejo en medio, nos daremos cuenta que el reflejo del rostro hace imperceptible la ausencia de la otra mitad.
Existen dos tipos de simetría, la simetría axial y la simetría central.
La simetría axial es cuando en una figura, al dividírla con una línea central (como muestra la imagen anterior), una de las mitades resultantes coinciden plenamente con la otra da las mitades.
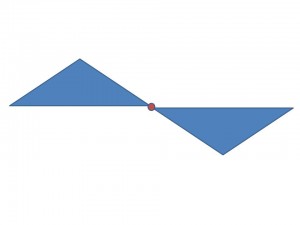
La simetría central es aquella en que la figura puede cambiar su orientación. Para ejemplificar una simetría central, podemos mencionar que es como si una imagen se reflejara dos veces, primero en un espejo vertical, luego en un espejo horizontal (como muestra la imagen que sigue).