Vectores
Descubre que es un vector, su diferencia con un escalar y la forma de presentarlos gráficamente.
Vectores y escalares
Un vector corresponde a una figura matemática que representa magnitud y dirección a la vez. Se representa geométricamente en forma de flecha y la manera como se define es a través de una letra, por ejemplo» a».
Se utiliza principalmente en física para representar movimientos o fuerzas. Se representa en un plano cartesiano cuando es un vector bidimensional y es expresado en un par ordenado a=(x,y) o bien a=(a1,a2). Sin embargo, un vector puede tener n dimensiones, en este caso su definición sería de la forma: a = (a1,a2,a3,…,an).
Dos vectores serán iguales entre si, si sólo si, sus elementos son iguales. Por ejemplo, si a=(a1,a2) y b=(b1,b2), entonces decimos que «a» es idéntico a «b», si sólo si, a1=b1 y a2=b2, en caso contrario, entonces decimos que «a» es distinto a «b».
Es importante diferenciar un vector de un escalar. En contraste al primero, que representa magnitud y dirección, un escalar corresponde a un número real que representa sólo magnitud. Ejemplos de escalares pueden ser rapidez y masa.
Representación gráfica de vectores
Como vimos previamente un vector puede representarse gráficamente mediante una flecha y ellas pueden ser representadas tanto en coordenadas rectangulares (plano cartesiano) o bien a través de coordenadas polares. (Para mayor información respecto a coordenadas rectangulares y polares ver sección «Repaso» al final del contenido)
La magnitud de un vector está representado por el largo de la flecha y su dirección se muestra a través de la orientación de ella.
A continuación veremos ejemplos de representaciones en ambas coordenadas.
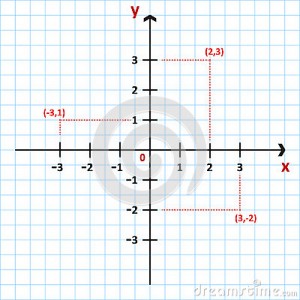
Coordenadas rectangulares:
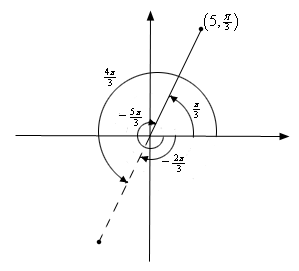
Coordenadas polares:
Suma de vectores
Suma
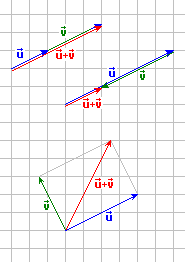
Considerando dos vectores a=(a1,a2) y b=(b1,b2) podemos decir que su suma será de la siguiente manera: a + b = (a1,a2) + (b1,b2) = (a1 + b1, a2 + b2)
Geométricamente si ambos vectores «a» y «b» son representados mediante respectivamente, entonces la suma de a + b es representada por como se muestra en la siguiente figura. Aún más, se demuestra que a + b = b + a.
Repaso
- Coordenadas rectangulares: Sistema de coordenadas que identifica la ubicación de un punto a través de un par ordenado (x,y) donde «x» e «y» representan las distancias a dos líneas perpendiculares, medidas en las mismas unidades. Cada línea perpendicular es conocida como eje y la intersección entre ambos es llamado origen, generalmente representado de la forma (0,0).
- Coordenadas polares: Sistema de coordenadas que identifica la ubicación de un punto mediante la distancia entre el mismo punto al polo (origen) y por el ángulo que se forma entre el eje polar (equivalente al eje x en un plano cartesiano) y la línea que une el polo y el punto. La forma en que se representa un punto en este sistema de coordenadas es: (r, ?), donde «r» representa la distancia entre el punto y el origen y «?» representa el ángulo formado.