Medidas de tendencia central

Las medidas de tendencia central son valores numéricos estadígrafos, que representan la tendencia de todos los datos estadísticos.

Las representaciones graficas nos demuestran de una vez, toda una serie de estadística o distribución de frecuencias. Pero en ocasiones se desea un valor numérico que presente a toda la población o muestra que se estudia. Estos números reciben el nombre de valores centrales de la distribución porque, a su alrededor se agrupan todos los demás. Es decir, se denominan medidas de tendencia central a los promedios o valores alrededor de los cuales se agrupan a todos los demás.

Las medidas de tendencia central más conocidas o importantes son: la media aritmética, la mediana y el modo o moda. También son, la media geométrica, la media armónica, la media cuadrática, la media bicuadrática y los cuartiles.

Índice

1 Media aritmética o promedio
2 Mediana
3 Modo o Moda
- 3.1 Métodos para calcular la moda
  - 3.1.1 Método directo o empírico:
  - 3.1.2 Método corregido o aproximado:
- 3.2 Importancia

Media aritmética o promedio

Es el cociente que resulta de dividir la suma de los valores de los datos entre el número de los mismos. Se simbolizan por M.

Cálculo en una distribución de frecuencias de datos no agrupados

Para calcular la media aritmética en una distribución de datos no agrupados, se suman todas las calificaciones, puntajes, datos, etc. Y el total se divide entre el número de ellos.

La fórmula para calcular la media aritmética (M) en datos no agrupados es:

$M = \frac{\sum x}{N}$

Dónde:

M = media aritmética
$\sum x$ = suma de datos
N = número de datos

Ejemplo: En los diferentes meses del año académico, un alumno obtuvo las calificaciones: 12, 16, 13, 8, 15 y 14 en la asignatura de Matemáticas. La calificación media de la asignatura será.

$M = \frac{12+16+13+8+15+14}{6} = \frac{78}{6} = 13$

Cálculo en una distribución de frecuencias de datos agrupados

Para calcular el valor de la media aritmética en una distribución de frecuencia de datos agrupados, se divide la suma total del producto entre las frecuencias (f) y los puntos medios o marcas de clase (pm), entre la suma total de frecuencias (f).

La fórmula para calcular la media aritmética en datos agrupados es:

$M = \frac{\sum f*pm}{\sum f}$

Dónde:

M= media aritmética
$\sum f*pm$ = suma de frecuencias por puntos medios o marcas de clases.
$\sum f$ = suma de frecuencias

Observemos la siguiente tabla de distribución de frecuencias de datos agrupados.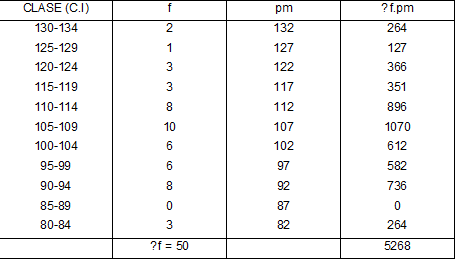

Reemplazamos la fórmula con los datos obtenidos tendremos:

$M = \frac{\sum f*pm}{50} = \frac{5268}{50}$ = 105.36

Quiere decir, que la nota promedio obtenida por el grupo de alumnos de la muestra es de 105,36.

Para obtener la media aritmética de esta distribución hemos seguido el procedimiento siguiente:

Se han determinado las clases (C.I) cuya amplitud o intervalo de clase es 5.
Se han indicado las frecuencias (f), o sea, las veces que se repite un dato o un valor.
Se han escrito los puntos medios o marca de clase (pm).
Se han determinado la frecuencia por un punto medio (f. pm), multiplicando cada frecuencia por su respectivo punto medio o marca de clase.
Se ha sumado la columna de f. pm
Luego, se aplicó la formula.

1.1.3 Importancia

Es importante porque:

La media aritmética es centro de la gravedad de la distribución, si los puntajes están distribuidos simétricamente.
Es la medida de tendencia central más estable.
Es el valor preferido en los cálculos estadísticos por ser el más fiable.
Es el procedimiento que representa mejor al grupo.

Mediana

Es el valor que divide a una distribución en dos partes iguales, se simboliza por Mdn.

1.1.1 Calculo en una distribución de frecuencias de datos no agrupados:

Se ordenan los puntajes en forma ascendente o descendente. Al determinar la mediana pueden presentar dos casos.

Si el número de datos es impar, la mediana será el dato que ocupa el centro de la distribución. Por ejemplo:

7, 9, 12, 16, 18, 19, 20

Observando la distribución, encontramos que la calificación 16 está ubicada en el centro; luego, la mediana es 16.

Si el número de datos es par, en este caso se suman las dos calificaciones que ocupan el lugar central y el resultado se divide entre 2. Por ejemplo:

19, 17, 16, 15, 13, 12, 10, 9

Observando la distribución, encontramos que los datos o puntajes que ocupan el lugar central son 15 y 13. Por tanto, la mediana será 14:

$M = \frac{15+13}{2}$ = 14

Es decir, la mediana es la media aritmética de los dos valores centrales.

Para determinar el lugar que ocupa el valor de la mediana en cualquiera de los dos casos, se utiliza la siguiente fórmula:

$M = \frac{N+1}{2}$

Dónde:

Mdn = mediana
N = número de datos.

NOTA: Para determinar la mediana a simple inspección se debe tener los datos completamente ordenados.

Cálculo en una distribución de frecuencias de datos agrupados

Para calcular la mediana, en una distribución de datos agrupados se aplica la siguiente fórmula:

$Mdn = Li + \frac{\frac{\sum f}{2} - fa}{f} * i$

Dónde:

$Mdn$ = mediana
$Li$ = límite inferior de la clase donde está ubicada la mediana.
$\sum f$ = suma total de las frecuencias.
$fa$ = frecuencia acumulada de la clase que precede a la clase que contiene la mediana.
$f$ = frecuencia de la clase que contiene a la mediana.
$i$ = amplitud de intervalo.

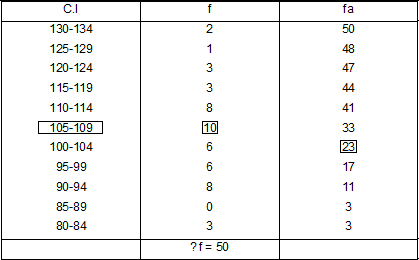
Observemos que en la siguiente tabla de distribución de frecuencias del cuadro N°2:

Antes de reemplazar la fórmula con los datos de la tabla de frecuencias, se ubica el lugar donde se halla la mediana, para lo cual se aplica la fórmula ya estudiada.

$M = \frac{N+1}{2}$ $M = \frac{50+1}{2} = 25.5$

Vemos que la mediana se encuentra en el intervalo de clase 105 – 109 porque, hasta su límite superior, suman 33 las frecuencias acumuladas y 25.5 está comprendida en este intervalo de clase.

Luego, para calcular el valor de la mediana sustituimos la fórmula con los datos respectivos.

$Mdn = Li + \frac{\frac{\sum f}{2} - fa}{f} * i$
$Mdn = 105 + \frac{\frac{50}{2} - 23}{10} * 5$
$Mdn = 105 + \frac{25 - 23}{10} * 5$
$Mdn = 105 + \frac{2}{10} * 5$
$Mdn = 105 + 1 = 106$

Importancia

Da conocer el punto medio exacto de la distribución, o sea, el punto correspondiente al 50% de la serie, cuando entre los datos hay valores extremos, ya que estos afectan el valor de la media aritmética.
Los valores extremos no la alteran.

Modo o Moda

Es el valor que se repite con mayor frecuencia. Se simboliza por Mo.

Métodos para calcular la moda

Para calcular el valor del modo se utilizan dos métodos.

Método directo o empírico:

En una distribución de frecuencias de datos no agrupados: Se determina observando que datos se repiten el mayor número de veces.
Ejemplo: 9, 10, 10, 12, 14, 14, 14, 16, 16, 18
En esta distribución el dato más frecuente es 14. Luego, 14 es el modo obtenido por el método empírico.
En una distribución de frecuencias de datos agrupados: Cuando los datos se agrupan en una tabla de distribución de frecuencias, el modo es el punto medio o marca de clase que contiene la mayor frecuencia. Por ejemplo, en nuestra tabla de distribución (cuadro N°2) el intervalo de la clase 105 – 109 tiene la mayor frecuencia. A este intervalo de clase se denomina clase modal. El punto medio de este intervalo de clase es 107. Luego, 107 es el modo obtenido por el método directo o empírico.

Método corregido o aproximado:

Se aplica la siguiente fórmula:

$Mo=Li+\frac{\Delta 1}{\Delta 1 +\Delta 2}*i$

Dónde:

$Li$ = límite inferior de la clase modal.
$\Delta 1$ = Es la diferencia de la frecuencia de la clase modal y la frecuencia de la clase inmediata superior.
$\Delta 2$ = Es la diferencia de la frecuencia de la clase modal y la frecuencia de la clase inmediata inferior.
$i$ = amplitud del intervalo

Sustituyendo la fórmula con los datos de nuestra tabla de frecuencia (N° 1 tenemos).

$Mo=105+\frac{10-8}{(10-8) +(10-6)}*5$
$Mo=105+\frac{2}{2+4}*5$
$Mo=105+\frac{2}{6}*5$
$Mo=105+0.33*5$
$Mo=105+1.65$
$Mo=106.65$

Importancia

Da a conocer en forma inmediata qué puntaje es el más frecuente.

Observaciones:

La moda no siempre existe en una distribución de frecuencias.
Puede existir 2 o más modas para una distribución de frecuencias.