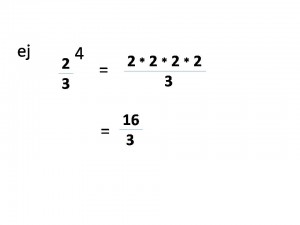Potencias de Base Racional

Resolución de potencias de base racional o fracción.

Recordando que una potencia se compone de una base (un número que se multiplica por sí mismo) y un exponente (las veces que el número se multiplica por sí mismo), una potencia de base racional implica que su base es una fracción.

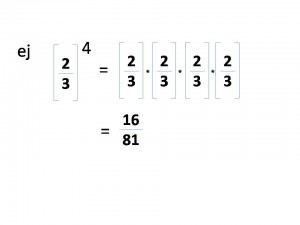
Es importante mencionar que no es lo mismo dos tercios elevado a cuatro, que dos elevado a cuatro, tercios. Ambos se resuelven de forma distinta como muestra el siguiente esquema:

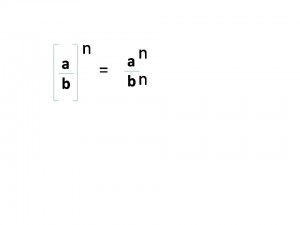
Potencia de Base Racional y Exponente Entero.

Como se mencionó anteriormente, una potencia con base racional y exponente entero quedaría:

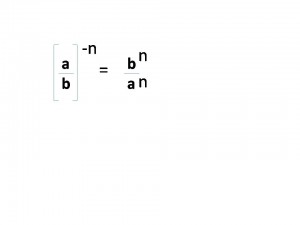
Potencia de Base Racional y Exponente Entero Negativo

Una potencia con exponente negativo y base racional quedaría de la siguiente forma:

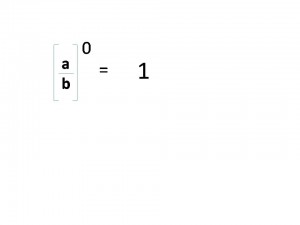
Potencia de Base Racional y Exponente Cero.

Una potencia con base racional y exponente cero, quedaría como muestra el siguiente esquema:

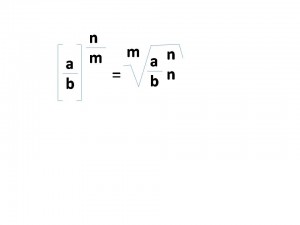
Potencia con Base Racional y Exponente Racional (Positivo)

Una potencia con base racional y exponente racional positivo quedaría de la siguiente manera:

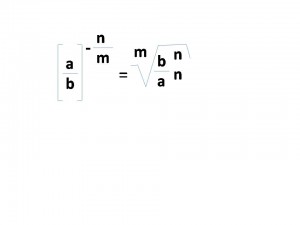
Potencia con Base Racional y Exponente Racional (Negativo).

Una potencia con base racional y exponente racional negativo quedaría de la siguiente forma:

Multiplicación y División de Potencias de Base Racional

Para multiplicar o dividir una potencia con base racional, se debe seguir la regla general de las Potencias,  (Ver Potencias). También es importante recordar que se debe considerar que para que se cumpla la regla mencionada en el artículo, las bases deben ser iguales.