La recta y su definición en el plano
Concepto de recta, ecuación de la recta, pendiente y cómo definir una recta en el plano cartesiano.
La recta es un concepto geométrico, a pesar que no es tan fácil expresar mediante el lenguaje su significado es una idea que la mayoría de la gente entiende ,se puede definir como un conjunto infinito de puntos que sigue o se traza a través de una misma dirección, por lo general se acostumbra denominarlas con letras minúsculas.
En geometría analítica es posible graficar y definir rectas en el plano cartesiano ,el cual corresponde a un sistema de referencia que se compone de dos ejes que se interceptan en el origen de este , los cuales se denominada «el eje y» o eje de las ordenadas y el «eje x» o eje de las abscisas.
Ecuación de la recta
La ecuación de la recta corresponde a una igualdad que vincula punto a punto los valores de las variables dependientes (o puntos en el eje y) con los de la variable independiente (o puntos en el eje x) además, es posible obtener de esta ecuación algunos de los elementos principales con los cuales se puede definir una recta , la ecuación se expresa de dos maneras las cuales se muestran a continuación:
Ecuación principal de la recta
y=mx+n
en donde:
m= pendiente de la recta.
n=coeficiente de posición o intersección con el eje y.
Ecuación general de la recta
Ax+By+C=0
donde:
pendiente =A/B
intersección con eje y = -C/B
Nota : si se tienen dos puntos de una recta es suficiente para obtener su gráfico.
Pendiente de una recta
La pendiente de una recta es uno de los elementos que permite definirla y corresponde a la inclinación que tiene esta con respecto al eje horizontal puede ser positiva o negativa se puede calcular teniendo dos puntos de la recta con la siguiente expresión:
Si se posee la ecuación de la recta también puede despejarse la pendiente quedando de la siguiente manera:
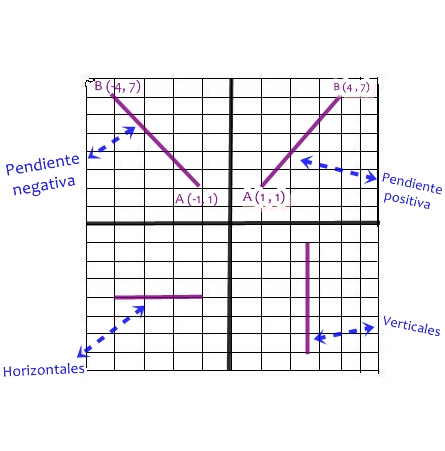
Las rectas con pendientes negativas y positivas es posible diferenciarlas visualmente teniendo su gráfico a continuación en la siguiente imagen se muestran rectas con pendiente positiva, negativa, cero e indefinida.
Una recta con pendiente cero corresponde a una recta horizontal o paralela al «eje x», pero si la recta es vertical o paralela al «eje y» queda indefinida su pendiente debido a que la división por cero no está definida en la matemática.
Algunas posiciones relativas que pueden tener dos rectas
-Rectas coincidentes: Si dos rectas tienen dos puntos en común se puede decir que son coincidentes en todo su recorrido y poseen la misma ecuación de la recta.
-Rectas secantes: Son rectas que se cortan o interceptan en un punto, para determinar el punto de intersección es necesario resolver el sistema de ecuaciones que determinan sus respectivas ecuaciones de la recta.
-Rectas paralelas: Son rectas que nunca se interceptan , si dos rectas son paralelas estas poseen la misma pendiente.
-Rectas perpendiculares: Son dos rectas que se interceptan con un ángulo recto o de 90 grados , si dos rectas son perpendiculares el producto de sus pendientes es -1.
Problema resuelto
A continuación un problema que permite poner en práctica la teoría expuesta:
Suponga que una recta «L1» pasa por los puntos P1=(1,1) y P2=(2,2) encuentre ecuación principal de la recta e identifique el coeficiente de posición y la pendiente.
La pendiente es posible determinarla de inmediato mediante la fórmula:
m=(y2-y1)/(x2-x1)= (2-1)/(2-1)=1
luego la ecuación queda:
y=mx+n , donde m =1
ahora reemplazamos «x «e «y» con los valores de «P1» y «m» con el valor ya calculado de la pendiente entonces se obtiene:
1=1*1+n , despejando n se tiene:
n=0
Así queda calculado el coeficiente de posición por lo cual se tiene que la ecuación queda de la siguiente manera:
y=x .