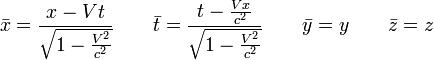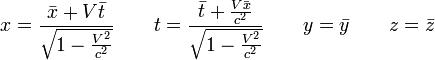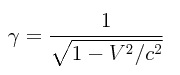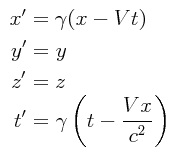Posición relativa
Conoce la relatividad del movimiento en relación con la forma de la trayectoria.
Como mencionamos en artículos anteriores, la descripción que se realice de un movimiento dependerá del sistema de referencia que utilice el observador para ello. La posición, como una de las características representativas de un movimiento, también variará de un sistema de referencia a otro, la naturaleza de este cambio fue estudiada en profundidad por Albert Einstein quien introduce el concepto de ‘posición relativa’.
Teoría de la relatividad
La teoría de la relatividad especial fue publicada por Albert Einstein en 1905. Einstein observó que la velocidad de la luz en el vacío era la misma en todos los sistemas de referencia inerciales, lo que sumado al hecho de que cualquier experimento se desarrollará de la misma manera en cualquier sistema de referencia inercial, le permitió establecer ecuaciones que permiten pasar de un sistema a otro de forma sencilla.
Sistemas de referencia y posición relativa
Consideremos dos sistemas de referencia, uno estático al que llamaremos S y otro en movimiento al que denominaremos S’. Si nos situamos en S veremos que el sistema S’ avanza por el eje x con velocidad constante v; es evidente entonces que un observador situado en S’ percibirá que el sistema S avanza por el eje x con velocidad constante –v.
En importante recordar que todos los sucesos físicos ocurren en el espacio-tiempo, por lo que, además de determinar sistemas de referencia y coordenadas debemos analizar la variable temporal, consideraremos que ambos sistemas están sincronizados, esto es, t = t’ = 0, cuando los orígenes de S y S’ coinciden.
De esta forma a cada cuerpo se le asignarán las coordenadas (t,x,y,z) en S y (t’,x’,y’,z’) en S’, para pasar de una a otra se utilizan las transformaciones de Lorentz.
Transformaciones de Lorentz
Llamamos transformaciones de Lorentz a un conjunto de ecuaciones que permiten relacionar la posición medida en un sistema de referencia con la que se obtendría en un segundo marco de referencia, estas relaciones son el sustento matemático de la teoría de la relatividad.
Las coordenadas atribuidas por observadores ubicados en los sistemas S y S’ antes descritos, están relacionadas por las siguientes expresiones:
Si pasamos del sistema S al S’:
Factor de Lorentz
El factor de Lorentz establece una relación simple que sirve para escribir las transformaciones de Lorentz de una forma más sencilla, esta relación es la siguiente:
Usando este factor, las transformaciones se escriben:
Es importante recordar que estas transformaciones son válidas sólo cuando a) t = t’ = 0 y b) el movimiento relativo de los sistemas de referencia sólo tiene una dirección, si cualquiera de estas condiciones no se cumplen, la forma de las ecuaciones se complica considerablemente.
Consecuencias relativistas:
- Dilatación del tiempo: Si un observador ubicado en un sistema de referencia estático y otro observador, ubicado en un sistema de referencia en movimiento, miden el tiempo transcurrido entre dos eventos, siempre el observador en movimiento medirá tiempos mayores. Este fenómeno es conocido como dilatación del tiempo.
- Contracción de longitudes: Contrario a lo que ocurre con el tiempo, en el caso de la medida de longitudes, los valores obtenidos por el observador en movimiento serán siempre menores que los medidos por el observador estático. A este fenómeno se le denomina contracción de longitud.
Aplicación
GPS
A diario utilizamos el GPS de nuestros celulares o automóviles para ubicarnos, para que ello sea posible existen 24 satélites orbitando la Tierra a una altura aproximada de 20.200 Km. Estos satélites demoran cerca de 12 horas en completar una vuelta completa alrededor de nuestro planeta lo que requiere que se desplacen a alta velocidad, pero no lo bastante alta para ser comparada con la de la luz. Pese a esto, el efecto relativista debe ser considerado por los ingenieros al momento de configurar los satélites, pues todos ellos están equipados con un reloj atómico de gran precisión capaz de medir pequeños intervalos de tiempo en los que se debe considerar el efecto de dilatación temporal. Si este efecto no es considerado, los sistema de GPS acumularían un error de cerca de 11 Km. al día.