Cilindro y Cono: área y volumen

Anteriormente aprendimos sobre la circunferencia, el círculo y calculamos aproximadamente el número \pi. Con esta nueva herramienta nos aventuraremos en un nuevo terreno: los volúmenes y áreas de cuerpos de revolución. El cilindro y el cono son dos ejemplos de ello.

 ¿Cómo se forman el cilindro y el cono?

El cilindro y el cono pertenecen a los comúnmente llamados cuerpos de revolución, que son los que se generan a partir de la rotación de ciertos polígonos sobre un eje, el que suele ser uno de sus lados.

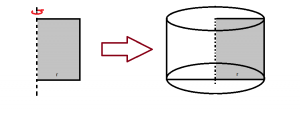
Si se hace rotar un rectángulo en torno a sus lados, obtenemos un cilindro.

fig-2

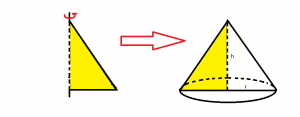
Si se hace rotar un triángulo rectángulo usando uno de sus catetos como eje obtenemos un cono.

Cilindrofig-2

Calculando el área y Volumen

Ya que anteriormente conocimos a nuestro amigo el número \pi, con su ayuda podemos calcular el área y el volumen de estos cuerpos. La idea detrás de estos conceptos es similar a la que ocupamos con los polígonos y los poliedros rectos: para obtener el área sumamos área de la base más área lateral y para el área multiplicamos base por altura por alto:

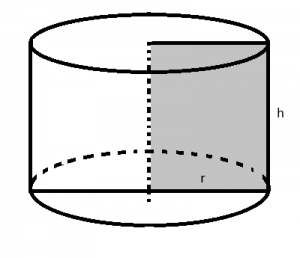
cilindrofig-3

Área del cilindro:

A_{Cil}=2\pi\cdot r^2+2\pi\cdot r \cdot h

Volumen del cilindro:

V_{Cil}=\pi\cdot r^2 \cdot h

 

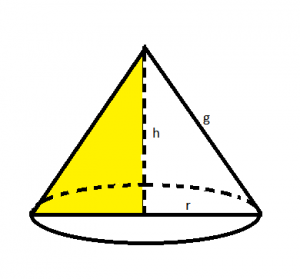
Área del cono:

A_{C}=\pi\cdot r\cdot g+\pi\cdot r^2

Donde g es la generatriz («lado» que se forma al rotar la hipotenusa)

Volumen del cono:

V_C=\frac{1}{3}\cdot \pi\cdot r^2 \cdot h

cilindrofig-4

Artículos Relacionados