Distancia entre puntos y punto medio

Analizaremos cómo calcular y demostrar la distancia entre puntos pertenecientes a un plano cartesiano. Además, punto medio entre un segmento determinado por dos puntos.

Distancia entre puntos

Para poder calcular la distancia entre dos puntos primeramente debemos conocer las coordenadas de estos puntos. Tomaremos dos puntos cualquieras para luego, a partir de estos generar un criterio para cualquiera sea el par de puntos a los que posteriormente calculemos la distancia.

Sean los puntos A=(x,y) y B=(w,z), dos puntos que pertenecen al primer cuadrante del plano cartesiano. Calcular la distancia entre ambos.

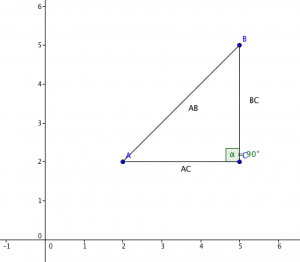
Para generar este calculo, deberemos ubicar los puntos en el plano cartesiano de manera que al generar el segmento que subtienden los puntos, este no sea paralelo a ningún eje coordenado. Una vez que se ubican los puntos, se debe ubicar un tercer punto referencial al que llamaremos C, que tendrá coordenadas C=(w,y) de manera de este punto genere un triángulo rectángulo y siendo precisamente el vértice del ángulo recto. Quedando precisamente un gráfico como el que veremos a continuación.

La idea de formar un triángulo rectángulo es que a partir de éste se puede utilizar el teorema de Pitágoras para calcular la distancia de su hipotenusa, que es el segmento particular que interesa. Podemos calcular la distancia de los catetos del triángulo rectángulo para así poder saber la distancia de la hipotenusa que representa la distancia entre el punto A y el punto B.

La distancia de los catetos AC será (w-x) y la del cateto BC será (z-y), por lo tanto, por teorema de Pitágoras definimos lo siguiente.

$\ AC^2+BC^2=AB^2$

$\ (w-x)^2+(z-y)^2=AB^2$

Por lo tanto el valor de la distancia AB será:

$\ AB = \sqrt{(w-x)^2+(z-y)^2}$

Ejemplo:

Calcular la distancia entre los puntos R=(5,6) y T=(2,2)

$\ RT = \sqrt{(2-5)^2+(2-6)^2}$

$\ RT = \sqrt{(-3)^2+(-4)^2}$

$\ RT = \sqrt{9+16}$

$\ RT = \sqrt{25}$

$\ RT = 5$

Punto Medio de un Segmento

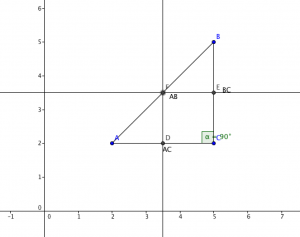
Para encontrar el punto medio del segmento utilizaremos los mismos puntos de la demostración anterior. Entonces, calcularemos el punto medio del segmento AB. Para eso utilizaremos el concepto de promedio, para calcular la distancia intermedia entre dos longitudes debemos calcular el promedio de estas. Si queremos saber cual es la distancia promedio entre 5 y 7, sumamos las variables y dividimos por 2, el resultado claramente es 6. Entonces ahora para calcular una distancia media entre dos puntos se deberá ocupar el mismo concepto. Se debe analizar por separado cada eje coordenado y así se poder encontrar el punto medio, según los puntos encontrados para cada eje coordenado.

Sean los puntos A=(x,y) y B=(w,z), dos puntos que pertenecen al primer cuadrante del plano cartesiano. Calcular el punto medio del segmento AB.

Calculamos la distancia media en ambos ejes coordenados, primero en el eje «x» y luego en el eje «y».

En el eje «x» el promedio de las longitudes será $\frac{x+w}{2}$

En tanto, el promedio en el eje y será $\frac{y+z}{2}$

Finalmente el punto medio es:

$(\frac{x+w}{2}, \frac{y+z}{2})$

Ejemplo:

Calcular el punto medio entre el punto(5,5) y el punto (9,3).

En el eje x el promedio de las longitudes será $\frac{5+9}{2}$

En tanto, el promedio en el eje y será $\frac{5+3}{2}$

Por lo tanto, el punto medio es:

$\ (7,4)$

Para calcular la distancia entre puntos y el punto medio es importante recordar cómo llegar a la fórmula general, eso permitirá consistencia y mayor fijación del contenido a la hora de estudiar.

Distancia entre puntos y punto medio

Distancia entre puntos

Punto Medio de un Segmento

Artículos Relacionados