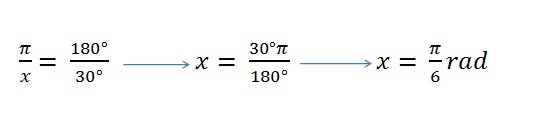El ángulo, los radianes y sus unidades de medición
Qué son los ángulos y cuáles son sus dos principales unidades de medición. Además, cómo transformar grados en radianes y cómo medir ángulos.
Los Ángulos son una herramienta matemática muy útil que se utilizan desde hace miles de años y que han sido de gran ayuda. Los ángulos son la base fundamental de un área de las matemáticas llamada Trigonometría y gracias a éstas, por ejemplo, el hombre pudo calcular grandes distancias sin la necesidad de recorrerlas, lo cual significó una gran revolución en la navegación. También es importante mencionar los avances que esto tuvo para la construcción, la astrología y en la guerra. A continuación aprenderás qué es un ángulo y cuáles son sus dos principales unidades de medición.
¿Qué es un ángulo?
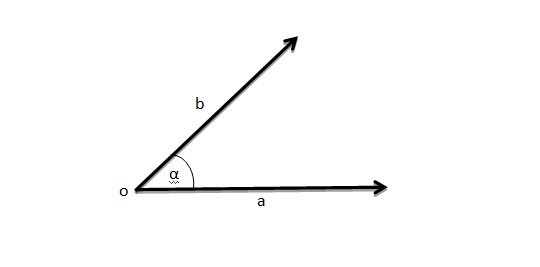
Imaginemos un plano en el espacio, para entenderlo mejor podemos usar una hoja de cuaderno en blanco. Ahora dibujemos dos semirrectas que partan desde un mismo punto, recordemos que las semirrectas son infinitas en un solo sentido por lo tanto se dibujan como si fueran una flecha, quedará algo parecido a la siguiente figura:
Como verán estas dos semirrectas, que ahora llamaremos lados (a y b), tienen un origen en común, que llamaremos vértice (o). La región comprendida entre ambos lados unidos por el mismo vértice será la que llamaremos ángulo, que se denota con una letra griega, en este caso usaremos la letra alfa (?).
¿Cuáles son las unidades para medir ángulos?
Existen varias unidades de medida para los ángulos, las más utilizadas por nosotros son el Grado sexagesimal (°) y el Radián (rad).
1) Grado sexagesimal
El grado sexagesimal se creó dividiendo una circunferencia en 360 partes iguales, el ángulo correspondiente a cada una de sus partes es un ángulo de un grado sexagesimal (1°).
Es importante saber que la necesidad de obtener un ángulo más pequeño que un grado sexagesimal (1°) se crearon los minutos (’) y los segundos (”) y equivalen de la siguiente forma:
- Un grado sexagesimal tiene 60 minutos (‘) y un minuto tiene 60 segundos (‘’).
- Por ejemplo, el ángulo 45° 30’ 55’’ se lee “cuarenta y cinco grados, treinta minutos, cincuenta y cinco segundos”.
2) El Radián
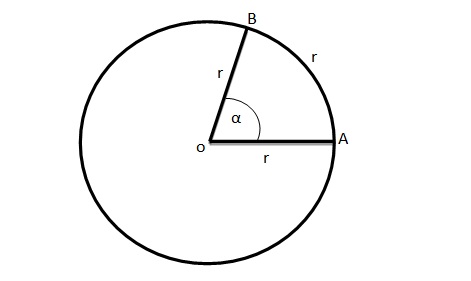
El Radián (rad) es la medida de un ángulo cuyo arco mide igual que el radio, para entender esto veamos la figura siguiente:
Tenemos una circunferencia donde el vértice del ángulo coincide con su centro (o) y que los lados de los ángulos ya no son semirrectas sino que ahora son dos radios (r) que describen un arco (AB) cuya longitud es igual a la del radio (r), cuando esto ocurre el ángulo (?) que contienen estos radios equivale a un radián 1 rad.
En términos generales se utiliza el número irracional pi (?) para hacer la equivalencia entre radianes y grados sexagesimales:
1? rad = 180°
En términos generales se utiliza el número irracional pi (?) para hacer la equivalencia entre radianes y grados sexagesimales:
1? rad = 180
¿Cómo transformamos grados a radianes?
Supongamos que tenemos un ángulo de 30 y queremos saber a cuantos radiantes equivale, con una simple ecuación podemos resolver esta incógnita:
Lo que nosotros sabemos es:
Y lo que queremos saber es (nuestra incógnita x):
¿Cómo medir ángulos?
Para medir ángulos existen una variada gama de instrumentos, el más común y simple de todos es el transportador que de seguro ya conocen; Este instrumento sirve para medir ángulos en grados sexagesimales y también sirve para construir ángulos.
Para medir un ángulo con el transportador lo primero es hacer coincidir el centro del transportador con el vértice del ángulo y luego hacer coincidir uno de sus lados con el grado cero (0º). De esta manera el otro lado del ángulo nos indicará con relativa exactitud que ángulo se está formando, digo relativa exactitud porque recordemos que hay minutos (‘) y segundos (‘’) y para eso existen instrumentos más sofisticados que pueden medir con mayor exactitud.
Una vez que ya sabemos cuánto mide el ángulo en grados sexagesimales, de ser necesario, podemos transformarlo a radianes como lo vimos anteriormente.