Función logarítmica

Te invitamos a descubrir el origen de los logaritmos, qué es una función logarítmica, sus propiedades y sus principales aplicaciones en la ciencia.

Historia¹

Fue a fines del siglo XVI en Merchiston, pequeña localidad cercana a Edinburgo, Escocia, donde John Napier inicio un trabajo de investigación entorno al uso práctico del cálculo numérico y que culminó luego en el año 1614 en la publicación de su obra «Mirifici Logarithmorum Canonis Descriptio», donde detallaba tablas logarítmicas y el uso práctico que se le podía entregar.

En 1615 Henry Briggs, profesor de matemáticas, luego de un trabajo en conjunto con Napier crea una tabla mejorada de logarítmos.

Función logarítmica.

La función logarítmica es aquella función que está compuesta de la siguiente manera: $y=\log_{a}x$ .

Donde «a» puede tomar cualquier valor tal que «a» es mayor a 0 y distinto de 1 y «x» es mayor a 0.

Es importante hacer notar que tanto «a» como «x» deben ser positivos, dado que no existe el logaritmo de 0 o de un número negativo.

Ésta función se dice que es la inversa de la función exponencial que tiene la siguiente forma $a^{y}=x$ .

En consecuencia a lo anterior, si $f(x)=a^{x}$ entonces, $f(x)^{-1}=\log_{a}x$ .

Tipos de logarítmos.

Existen dos tipos de logarítmos, común y natural.

Logaritmo común: $log_{10}x$ y usualmente se escribe $log x$ .
Logarítmo natural: $log_{e}x$ y usualmente se escribe $ln x$ .

Formas función logarítmica

La función logarítmica puede tener dos formas posibles dependiendo de los valores que tome «a».

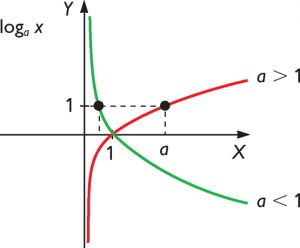
Como se puede apreciar en la siguiente imagen, si «a» toma valores entre 0 y 1, esto es 0<a<1, la función logarítmica toma la forma de la línea verde en el plano cartesiano. Por otro lado, si «a» toma valores mayores a 1, esto es a>1, la función logarítmica toma la siguiente forma en el plano cartesiano.

Propiedades de logarítmos

$log_{a}(xy)=log_{a}(x)+log_{a}(y)$
$log_{a}(\frac{x}{y})=log_{a}(x)-log_{a}(y)$
$log_{a}(\frac{xy}{yz})=\frac{log_{a}({x})+log_{a}({y})}{log_{a}({y})+log_{a}({z})}$

Evaluando logarítmos

Como se puede desprender de lo señalado anteriormente, la coordenada (1,0) siempre estará incluida en la función $f(x)=\log_{a}x$ independiente de los valores que tome «a». Lo mismo sucede con la coordenada o punto (a,1). Esto se ve reflejado de la siguiente manera:

$log_{a}1=0$ , porque $a^{0}=1$

$log_{a}a=1$ , porque $a^{1}=a$

Más concretamente, sabiendo que las funciones $log_{a}x$ y $a^{x}$ son inversas entre ellas, podemos concluir de forma general que: $f(x)=log_{a}(a^{x})$ y $a^{log_{a}x}=f(x)$

Aplicaciones de funciones logarítmicas.

Actualmente las funciones logarítmicas son aplicadas en un sinfín de actividades. A continuación se nombran algunos ejemplos de sus usos:

Sismología, en el cálculo de la intensidad de sismos o terremotos a través de la escala de Richter.
Química, en el cálculo del pH de una solución.
Acústica, en el cálculo de los decibeles para determinar la intensidad de un sonido.

Referencias:

¹»Cálculo con geometría analítica», Edwards y Penny. Editorial prentice Hall, cuarta edición.