Los Conjuntos
Un conjunto es una agrupación de objetos, que poseen alguna característica en común. Pero no sólo nos referimos a cosas físicas, como lápices, libros, calculadoras, etc., sino también a elementos abstractos como números ó letras, entre otros.
A los objetos se les llama elementos del conjunto.
Si tenemos el siguiente conjunto:
C = {1, 2, 3, 4}, decimos que los elementos del conjunto “C” son los números: 1, 2, 3 y 4.
Con frecuencia, utilizamos letras mayúsculas A, B, C… para designar al conjunto, y letras minúsculas a, b, c, d…. para referirnos a los elementos que forman parte de ese conjunto. Todos los conjuntos se escriben entre llaves {…}.
Determinación de un Conjunto
Los conjuntos pueden definirse por extensión o por comprensión.
Extensión
Se escriben los elementos que forman parte del conjunto, uno por uno separados por una coma y entre paréntesis de llaves.
C = {norte, sur, este, oeste}
Comprensión
Decimos que un conjunto es determinado por comprensión, cuando se da una propiedad que se cumpla en todos los elementos del conjunto y sólo ellos.
C = {x / x es un punto cardinal}
Y se lee de la siguiente manera: “C” es el conjunto de todos los elementos x, tal que x es uno de los puntos cardinales.
Ejemplos:
- A = { x/x es una consonante}
- B = { x/x es un número impar menor que 10}
- C = { x/x es una letra de la palabra feliz}
Para definir un conjunto por compresión, es necesario saber algunos símbolos matemáticos:
1. < “menor que”
2. > “mayor que”
3. / “tal que”
4. ^ “y”
Decimos que dos conjuntos son iguales, sólo si contienen los mismos objetos.
Ejemplo:
- A = { a, e, i, o, u }
- A = { a, e, i, o, u, a}
- C = {x / x es una vocal}
Como se puede ver, los tres conjuntos (A, B y C) son iguales, por lo que podemos darnos cuenta que podemos describir un mismo conjunto de diferentes maneras.
| Ejemplos por Extensión | Ejemplos por Comprensión |
| A = { a, e, i, o, u} | A = { x/x es una vocal } |
| B = { 1, 3, 5, 7, 9} | B = { x/x es un número impar menor que 10 } |
| D = { f, e, l, i, z} | D = { x/x es una letra de la palabra feliz } |
| E = { b, c, d, f, g, h, j, k . . . } | E = { x/x es una consonante } |
| G = {venus, marte,…} | G = {x/x es un planeta} |
Relación entre Conjuntos
Un elemento puede pertenecer o no a un conjunto dado.
Para señalar se un elemento pertenece a un conjunto se usa el símbolo 
y, para decir que no pertenece el símbolo 
.
Ejemplo:
Sea A = { a, e, o, u }
- a 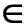A …se lee: a pertenece al conjunto A
- i 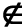A …se lee: i no pertenece al conjunto A
Un conjunto puede ser o no subconjunto de otro
Un conjunto A es subconjunto de B (o está incluido en B), si todos los elementos de A pertenecen a B.
Notación: A 
B; se lee: A es subconjunto de B
Tipos de conjuntos
Conjunto Vacío
Es el que no posee elementos. También se le llama conjunto nulo. Generalmente se le representa por los símbolos: 
ó { }
B = ó B = { } se lee: B es el conjunto vacío ó B es el conjunto nulo
Conjunto Unitario
Es el que tiene un único elemento
Conjunto Universo
Se llama así al conjunto formado por todos los elementos
Ejemplo
U = {a, e, i, o, u}
A={a, e}
B={a, i, o, u}
Conjunto Finito
Se llama así al conjunto al cual podemos nombrar su último elemento
Ejemplo: D ={x/x es día de la semana}
Es finito porque sabemos cuáles son todos los días de la semana.
Conjunto Infinito
Se denomina así, ya que no podemos nombrar su último elemento.
Conjuntos disjuntos
Son aquellos que no poseen ningún elemento común.
Operaciones de Conjuntos
1.- Intersección
A 
C= Es el conjunto formado por los elementos comunes de A y C
2.- Unión
B 
A = Es el conjunto formado por los elementos que pertenecen tanto a B como a A
3.- Diferencia
A – D = Conjunto formado por todos los elementos de A que no pertenecen a D
4.- Complemento
B´ = Es el conjunto formado por todos los elementos del universo, que no pertenecen a B