Productos Notables

Los productos notables son multiplicaciones de dos expresiones algebraicas que pueden resolverse por medio de ciertas reglas sin efectuar las multiplicaciones correspondientes. A continuación se muestran cada uno de estos productos, su fórmula, una breve explicación y un ejemplo práctico.

Binomio al cuadrado

Fórmula

$(a+b)^2=a^2+2ab+b^2$

Explicación

Primero elevamos al cuadrado el primer término.
$(a)^2=(a)(a)=a^2$
Luego multiplicamos por 2 el producto de los términos.
$2(a)(b)=2ab$
Por último elevamos al cuadrado el segundo término.
$(b)^2=(b)(b)=b^2$

Ejemplo

Resolver $(2/3 m^2-3/4 mn^3 )^2$

Solución

Primero elevamos al cuadrado el primer término.
$(2/3 m^2)^2=(2/3 m^2 )(2/3 m^2 )=4/9 m^4$
Luego multiplicamos por 2 el producto de los términos.
$2(2/3 m^2 )(-3/4 mn^3 )=-m^3 n?^3$
Por último elevamos al cuadrado el segundo término.
$(3/4 mn^3)^2=(3/4 mn^3 )(3/4 mn^3 )=9/16 m^2 n^6$
Y escribimos el resultado:
$(2/3 m^2-3/4 mn^3 )^2=4/9 m^4-m^3 n^3+9/16 m^2 n^6$

Binomio al cubo

Fórmula

$(a+b)^3=a^3+3a^2 b+3ab^2+b^3$

Explicación

Primero elevamos al cubo el primer término.
$(a)^3=(a)(a)(a)=a^3$
Luego multiplicamos por 3 el producto del cuadrado del primer término por el segundo término.
$3(a)^2 (b)=3a^2 b$
Luego multiplicamos por 3 el producto del primer término por el cuadrado del segundo término.
$3(a) (b)^2=3ab^2$
Por último elevamos al cubo el segundo término.
$(b)^3=(b)(b)(b)=b^3$

Ejemplo

Resolver $(2/3 m^2-3/4 mn^3 )^3$

Solución

Primero elevamos al cuadrado el primer término.
$(2/3 m^2)^3=(2/3 m^2 )(2/3 m^2 )(2/3 m^2 )=8/27 m^6$
Luego multiplicamos por 3 el producto del cuadrado del primer término por el segundo término.
$3(2/3 m^2 )^2 (-3/4 mn^3 )=3(4/9 m^4 )(-3/4 mn^3 )=-m^5 n^3$
Luego multiplicamos por 3 el producto del primer término por el cuadrado del segundo término.
$3(2/3 m^2 ) (-3/4 mn^3 )^2=3(2/3 m^2 )(9/16 m^2 n^6 )=9/8 m^4 n^6$
Por último elevamos al cubo el segundo término.
$(-3/4 mn^3)^3=(-3/4 mn^3 )(-3/4 mn^3 )(-3/4 mn^3 )=-27/64 m^3 n^9$
Y escribimos el resultado:
$(2/3 m^2-3/4 mn^3 )^3=8/27 m^6-m^5 n^3+9/8 m^4 n^6-27/64 m^3 n^9$

Binomios conjugados

Fórmula

$(a+b)(a-b)=a^2-b^2$

Explicación

Primero elevamos al cuadrado el primer término.
$(a)^2=(a)(a)=a^2$
Luego elevamos al cuadrado el segundo término.
$(b)^2=(b)(b)=b^2$
Y por último hacemos la diferencia y listo.
$a^2-b^2$

Ejemplo

Resolver $(2/3 m^2+3/4 mn^3 )(2/3 m^2-3/4 mn^3 )$

Solución

Primero elevamos al cuadrado el primer término.
$(2/3 m^2)^2=(2/3 m^2 )(2/3 m^2 )=4/9 m^4$
Luego elevamos al cuadrado el segundo término.
$(-3/4 mn^3)^2=(-3/4 mn^3 )(-3/4 mn^3 )=9/16 m^2 n^6$
Y por último hacemos la diferencia y listo.
$(2/3 m^2+3/4 mn^3 )(2/3 m^2-3/4 mn^3 )=4/9 m^4-9/16 m^2 n^6$

Trinomio al cuadrado

Fórmula

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Explicación

Primero elevamos al cuadrado el primer término.
$(a)^2=(a)(a)=a^2$
Luego elevamos al cuadrado el segundo término.
$(b)^2=(b)(b)=b^2$
De la misma manera elevamos al cuadrado el tercer término.
$(c)^2=(c)(c)=c^2$
Posteriormente multiplicamos por 2 el producto de los dos primeros términos.
$2(a)(b)=2ab$
A continuación multiplicamos por 2 el producto del primero y tercer términos.
$2(a)(c)=2ac$

Y por último multiplicamos por 2 el producto de los dos últimos términos.
$2(b)(c)=2bc$

Ejemplo

Resolver $(2/3 m^2+ 5/8 mn-3/4 mn^3 )^2$

Solución:

Primero elevamos al cuadrado el primer término.
$(2/3 m^2)^2=(2/3 m^2 )(2/3 m^2 )=4/9 m^4$
Luego elevamos al cuadrado el segundo término.
$(5/8 mn)^2=(5/8 mn)(5/8 mn)=25/64 m^2 n^2$
De la misma manera elevamos al cuadrado el tercer término.
$(-3/4 mn^3)^2=(-3/4 mn^3 )(-3/4 mn^3 )=9/16 m^2 n^6$
Posteriormente multiplicamos por 2 el producto de los dos primeros términos.
$2(2/3 m^2 )(5/8 mn)=5/6 m^3 n$
A continuación multiplicamos por 2 el producto del primero y tercer términos.
$2(2/3 m^2 )(-3/4 mn^3 )=-m^3 n^3$
Y por último multiplicamos por 2 el producto de los dos últimos términos.
$2(5/8 mn)(-3/4 mn^3 )=-15/16 m^2 n^4$
Y escribimos el resultado:
$(2/3 m^2+ 5/8 mn-3/4 mn^3 )^2=4/9 m^4+25/64 m^2 n^2+9/16 m^2 n^6+5/6 m^3 n-m^3 n^3-15/16 m^2 n^4$

Producto de binomios de la forma $(x+a)(x+b)$

Formula

$(x+a)(x+b)=x^2+(a+b)x+ab$

Explicación

Primero elevamos al cuadrado el primer término.
$(x)^2=(x)(x)=x^2$
Luego sumamos las constantes a y b y lo multiplicamos por x.
$(a+b)x$
Por último multiplicamos las constantes a y b.
$ab$

Ejemplo

Resolver $(m+3/4)(m-1/2)$

Solución

Primero elevamos al cuadrado el primer término.
$(m)^2=(m)(m)=m^2$
Luego sumamos las constantes 3/4 y -1/2 y lo multiplicamos por m.
$[3/4+(-1/2)]m=(3/4-1/2)m=1/4 m$
Por último multiplicamos las constantes 3/4 y -1/2 .
$(3/4)(-1/2)=-3/8$
Y escribimos el resultado:
$(m+3/4)(m-1/2)=m^2+1/4 m-3/8$

Producto de binomios de la forma 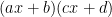$(ax+b)(cx+d)$

Formula

$(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$

Explicación

Primero multiplicamos los términos con literal x.
$(ax)(cx)=acx^2$
Luego sumamos el producto de los coeficientes de los extremos y los términos medios y los multiplicamos por x.
$[(a)(d)+(b)(c)]x=(ad+bc)x$
Por último multiplicamos las constantes b y d.
$(b)(d)=bd$

Ejemplo

Resolver $(2/3 m+3/4)(1/3 m-1/2)$

Solución

Primero multiplicamos los términos con literal m.
$(2/3 m)(1/3 m)=2/9 m^2$
Luego sumamos el producto de los coeficientes de los extremos y los términos medios y los multiplicamos por m.
$[(2/3)(-1/2)+(3/4)(1/3)]m=(-1/3+1/4)m=-1/12 m$
Por último multiplicamos las constantes 3/4 y -1/2 .
$(3/4)(-1/2)=-3/8$
Y escribimos el resultado:
$(2/3 m+3/4)(1/3 m-1/2)=2/9 m^2-1/12 m-3/8$

Productos Notables

Binomio al cuadrado

Fórmula

Explicación

Ejemplo

Solución

Binomio al cubo

Fórmula

Explicación

Ejemplo

Solución

Binomios conjugados

Fórmula

Explicación

Ejemplo

Solución

Trinomio al cuadrado

Fórmula

Explicación

Ejemplo

Solución:

Producto de binomios de la forma

Formula

Explicación

Ejemplo

Solución

Producto de binomios de la forma

Formula

Explicación

Ejemplo

Solución

Artículos Relacionados

Producto de binomios de la forma $(x+a)(x+b)$

Producto de binomios de la forma $(ax+b)(cx+d)$