Rectas
Conoce la recta, la ecuación de la recta, la recta en el plano cartesiano y el sistema de coordenadas espaciales.
Definición de Recta
Para configurar una línea recta, es necesario de dos puntos. La distancia más corta entre estos dos puntos, es una línea recta.
Una recta está configurada por infinitos puntos.
Una recta solo tiene una dimensión (largo), tampoco posee ni principio ni fin, se prolonga infinitamente.
Las rectas se suelen nombrar con una letra imprenta minúscula.
Semi Recta. Una semi recta es una recta que al dividirla en dos y analizando una de las dos partes, ésta tiene un principio. La semi recta en uno de sus extremos se prolonga infinitamente.
Para configurar una recta en un plano, elemento que posee dos dimensiones (largo y ancho) es necesario de identificar dos pares dentro de un plano, para esto se utiliza el plano cartesiano.
Recta en un Plano Cartesiano.
El plano cartesiano, es un sistema de coordenadas compuesto por dos líneas rectas numeradas, una verticalmente conocido como eje «Y» o eje de las abscisas; y otra horizontalmente conocido como eje «X» o eje de las ordenadas. Las abscisas y las ordenadas pueden estar numeradas de uno en uno, dos en dos, cinco en cinco, diez en diez, etc. Se pueden numerar con intervalos constantes dependiendo de la comodidad necesaria para dibujar los puntos y rectas en el plano.
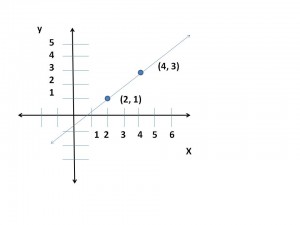
La recta en un plano cartesiano se configura con dos puntos, que usualmente se les llama pares ordenados. Los pares ordenados tienen primero una componente en «X» y luego les sigue una componente en «Y» y se anotan como (X,Y) ejemplo: (4,3) y (2,1); si anotamos estos dos puntos en un plano cartesiano y luego trazamos una línea recta entre ellos, tendríamos lo siguiente:
Recta en el sistema de coordenadas cartesianas espaciales.
Un sistema de coordenadas espaciales tiene tres dimensiones (largo, ancho y alto). Un sistema de coordenadas en el espacio incorpora un tercer eje, llamado eje «Z» o eje de cota de punto. Este eje también se conoce como eje profundidad.
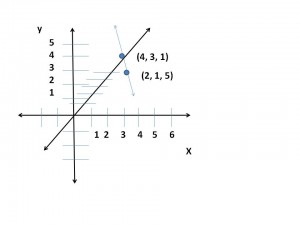
Para configurar una recta en un sistema de coordenadas espaciales es necesario incorporar a la demarcación del punto el elemento «Z» ejemplo (X,Y,Z): (4,3,1) y (2,1,5).
Ecuación de la Recta.
La ecuación de la recta, en un sistema de coordenadas cartesianas en un plano tiene dos componentes («x» e «y»), en un sistema de coordenadas cartesianas espaciales tiene tres variables («x», «y» y «z»). Para efectos educativos, estudiaremos la ecuación de la recta en un sistema de coordenadas en un plano:
Ejemplo de ecuación de la recta en coordenadas en un plano:
y = 2x + 3,
esto significa que «y» es igual a dos factor de «x» más tres.
A continuación algunos elementos de análisis lineal:
- Encontrar puntos para dibujar la recta.
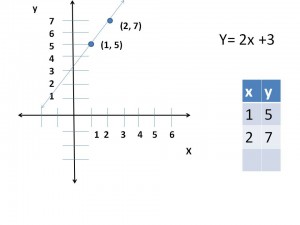
Para encontrar puntos en la recta, se le debe asignar valores a «X», por ejemplo, si X = 1, dos por uno es dos y más tres es cinco, o sea, y = 5. Esto es, un punto sería (1, 5)
Dibujando otro punto se puede dibujar la recta, por ejemplo, si X = 2, resolviendo, Y = 7, o sea el punto sería (2, 7).
- Encontrar la pendiente de la recta.
Una vez obtenido dos puntos pertenecientes a la recta, se obtiene la diferencia de la componente «Y»
de ambos puntos, y se divide por la diferencia de la componente «X» de ambos puntos.
Por ejemplo, obtenidos (1,5) y (2,7) la pendiente sería (5-7)/(1-2), la pendiente es 2.
Si la pendiente es positiva, entonces es ascendente.
Si la pendiente es negativa, entonces es descendente.
Si la pendiente es igual a cero, entonces es paralela al eje de las ordenadas.
Si la pendiente es infinita esto significa que la recta es paralela al eje de las abscisas.
- Encontrar en qué punto la recta corta el eje de las abscisas.
Para encontrar el punto en que la recta corta el eje «Y», se iguala «X» a 0, o sea si X=0, resolviendo, Y=3. El punto sería (0, 3).
- Encontrar en qué punto la recta corta el eje de las ordenadas.
Se realiza la misma operación, pero en este caso, se realiza con Y=0 y se despeja «X», en el caso del ejemplo, el resultado sería: x= -1,5, el punto quedaría (-1,5 , 0).