Relaciones lineales
Conoce que es una función lineal y una función afín, cuáles son sus características y en que se diferencian, además de la representación gráfica de cada una de éstas.
Es importante que recuerdes la noción de función, interiorizando los conceptos y características de ésta, para eso te recomendamos que visites nuestro capítulo de nociones de funciones.
Función lineal
Este tipo de función se caracteriza por dos cosas:
- La imagen de una suma de pre-imágenes debe ser igual a la suma de las imágenes generadas sumadas por separado. Es decir, matemáticamente hablando.
f(x + y) = f(x) + f(y)
- Además, se debe considerar que la imagen de una pre-imagen multiplicada por un escalar es igual a la imagen multiplicada por el mismo escalar. Es decir, matemáticamente hablando.
f(k*x) = k*f(x)
Consideremos la función f(x)=5x para analizar si es o no es una función lineal. Para eso esta función deberá cumplir con los dos pasos anteriormente explicados.
- f(x + y) = 5(x + y ) = 5x + 5y = f(x) + f(y), por lo tanto se cumple la primera condición.
- f(kx) = 5(kx), ocupando asociatividad obtendremos (5k)x, ahora conmutamos y tenemos (k5)x, volvemos a asociar y queda finalmente k(5x) y eso es lo mismo que kf(x), por lo tanto se cumple la segunda condición.
Como se cumple la condición 1 y 2, podemos decir que f(x) = 5x es una función lineal.
Función afín
En palabras simples, podemos definir una función afín como una función lineal que se desplaza una cierta cantidad de términos. Consideremos el siguiente ejemplo:
Un peatón se desplaza a 5 kilómetros por hora en dirección al norte, consideremos que partió a 10 kilómetros al norte de su casa. Cuál será la función que modele la distancia que se encuentra el peatón de su casa al pasar las horas?
La función que modela la situación es f(x) = 5x +10, con x representando la cantidad de horas. Se parece mucho a la función lineal que vimos anteriormente, sin embargo a esta se le suma 10.
Analicemos si es o no una función lineal, analizando el cumplimiento de los pasos 1 y 2.
- f(x+y) = 5(x+y) +10 = 5x +5y +10, pero es distinto de f(x)+ f(y).
Como no cumple el paso uno diremos que no es una función lineal.
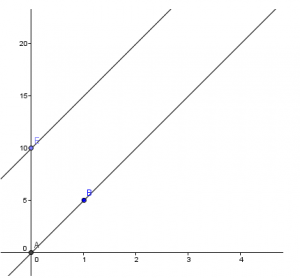
Analicemos gráficamente estas dos situaciones y veamos que sucede.
Notarás que las funciones son iguales en su pendiente sin embargo, existe una diferencia entre ellas que precisamente son 10 unidades que es el coeficiente de posición de la segunda función.
En resumen, una función lineal será una función de primer grado que pasará por el punto (0,0), en tanto una función afín será una función de primer grado que no pasará por el punto (0,0) es decir que no pasará por el origen.
Finalmente, escribiremos matemáticamente lo anterior:
Función Lineal: f(x) = mx , con m igual a la pendiente de la recta
Función afín: f(x) = mx + n , con m igual a la pendiente de la recta y n igual al coeficiente de posición.