Sistema de ecuaciones de 2×2

Encontraremos la solución a los sistemas de ecuaciones, desarrollando gráficamente y teóricamente las nociones de sistemas a partir de la visualización de rectas en el plano cartesiano.

¿Qué es un sistema de ecuaciones?

Un sistema de ecuaciones es un método para encontrar respuesta a situaciones en las que tenemos dos o más fenómenos expresados matemáticamente cómo ecuaciones que afectan sobre un mismo tema. Si lo apreciamos bajo la perspectiva geométrica podemos establecer que un sistema de ecuaciones nos ayuda a encontrar lugares geométricos particulares dentro de un sistema de referencia.

Para comprender el funcionamiento del sistema de ecuaciones de 2×2, tendremos que relacionar de manera significativa la parte de la ejecución para encontrar la respuesta como la parte geométrica que demuestra en el plano cartesiano la ejecución de un sistema de ecuaciones de 2×2. Es importante que tengas presente que cada ecuación de primer grado que puedas establecer bajo un contexto de dos variables, podrá ser descrito también en el plano cartesiano como una recta.

Un clásico ejercicio  de sistemas de ecuaciones es cuando un objeto alcanza a otro en su trayectoria, analicemos el siguiente ejemplo.

Dos autos realizan un viaje a la playa, el primero parte a las 10:00 y viaja a una velocidad promedio de 75 km/h, el segundo parte a las 11:00 y viaja a una velocidad promedio 100 km/h. ¿En cuánto tiempo y a qué distancia se encontrarán?

Lo primero que debemos hacer es plantear nuestras ecuaciones. La primera será y=75x donde que «x» son las horas e «y» la distancia recorrida, la segunda ecuación presenta mayor dificultad para plantearla puesto que el auto parte una hora después que el primero, por lo tanto debemos acomodar la ecuación para que a la primera hora el auto no recorra ni un kilómetro, por lo que la ecuación quedará y=100x -100 donde «x» son las horas e «y» la distancia recorrida.

Por lo tanto, nuestras ecuaciones serán:

y = 75x

y = 100x – 100

Utilizaremos el método de igualación para resolver el sistema, puedes revisar la publicación solución de ecuaciones lineales para recordar. A continuación igualamos la variable y.

75x = 100x – 100

25x=100

X=4

Por lo tanto si x=4 podemos reemplazar en cualquiera de las dos ecuaciones anteriores para encontrar la variable «y».

y = 75*4=300

Definimos anteriormente que la variable «x» establece las horas que transcurren y también que la variable define la cantidad de kilómetros que recorrerán los autos. Por lo tanto, según lo establecidó podemos decir que los autos se juntarán al pasar 4 horas desde la salida del primero y pasarán 300 km hasta el punto de encuentro.

Intersección en el plano cartesiano

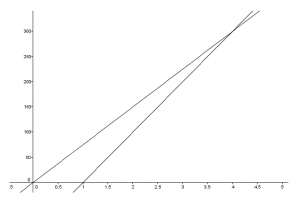
Podemos confirmar el cálculo que realizamos con el análisis gráfico en el plano cartesiano, para eso lo que queremos comprobar es que las rectas que representan las trayectorias de los autos se intersectarán en el punto (4,300). Analicemos el gráfico para afirmar lo anterior.

Como puedes ver las rectas se intersectan en el punto (4,300) lo que afirma gráficamente nuestra hipótesis. Es importante desarrollar los sistemas de 2×2, tanto en los resultados como la representación geométrica para posteriormente entregar una buena interpretación de éstos.